Logistic Regression and Gradient Descent from Scratch

In this project, I implemented a logistic regression model from scratch and update its gradients by following stochastic gradient descent approach.

For the full pipeline:

Initialization

The dataset has 2 features. When I checked the training labels, I saw labels were either -1 or 1. So, I decided to use tanh as the scaler function, instead of the σ. So, in this problem:

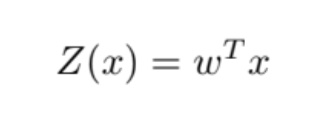
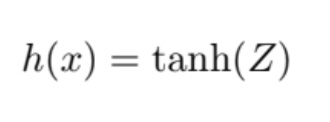
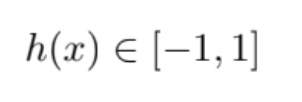
and my loss function is (since I am using tanh, I choose this loss function. It gaves negative or zero into the logarithm if I use other popular logistic loss function):

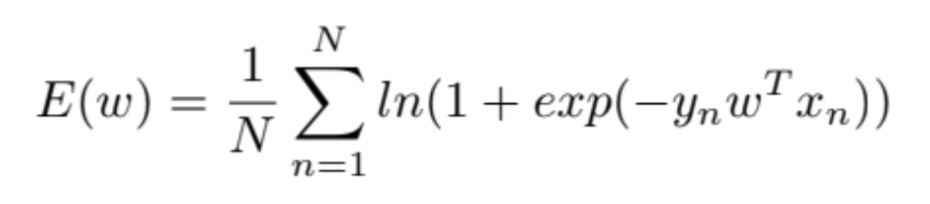
Training

For the training part, I started with random initialized weights w1, w2, b. For each epoch, i traversed in the shuffled dataset (I shuffled the indices of the dataset actually, not the dataset itself.) and in each iteration in the epoch, for each data point I randomly chose, I updated the weights. To take the partial derivative of the loss function and update the related weights (partial derivative of loss function according to w1 to update w1, etc.), I used chain rule.

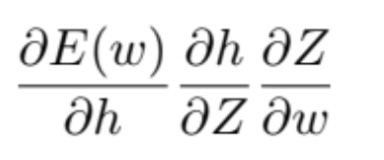
for w1, the gradient is

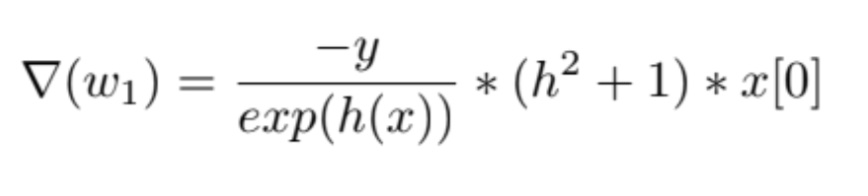
for w2, the gradient is

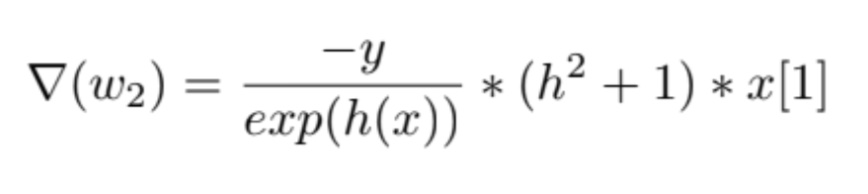
and for b, gradient is

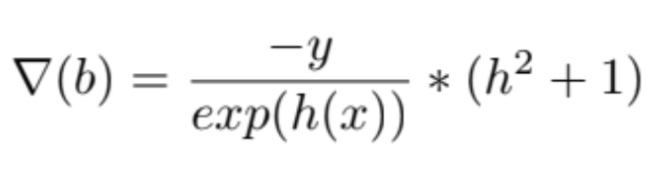
At the end of the each iteration, I updated the weights and the bias by the following formula:

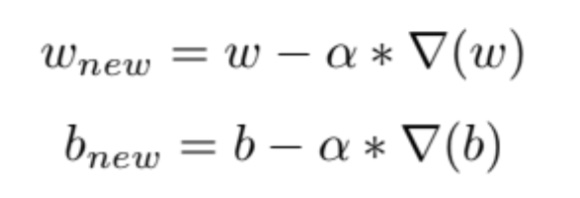
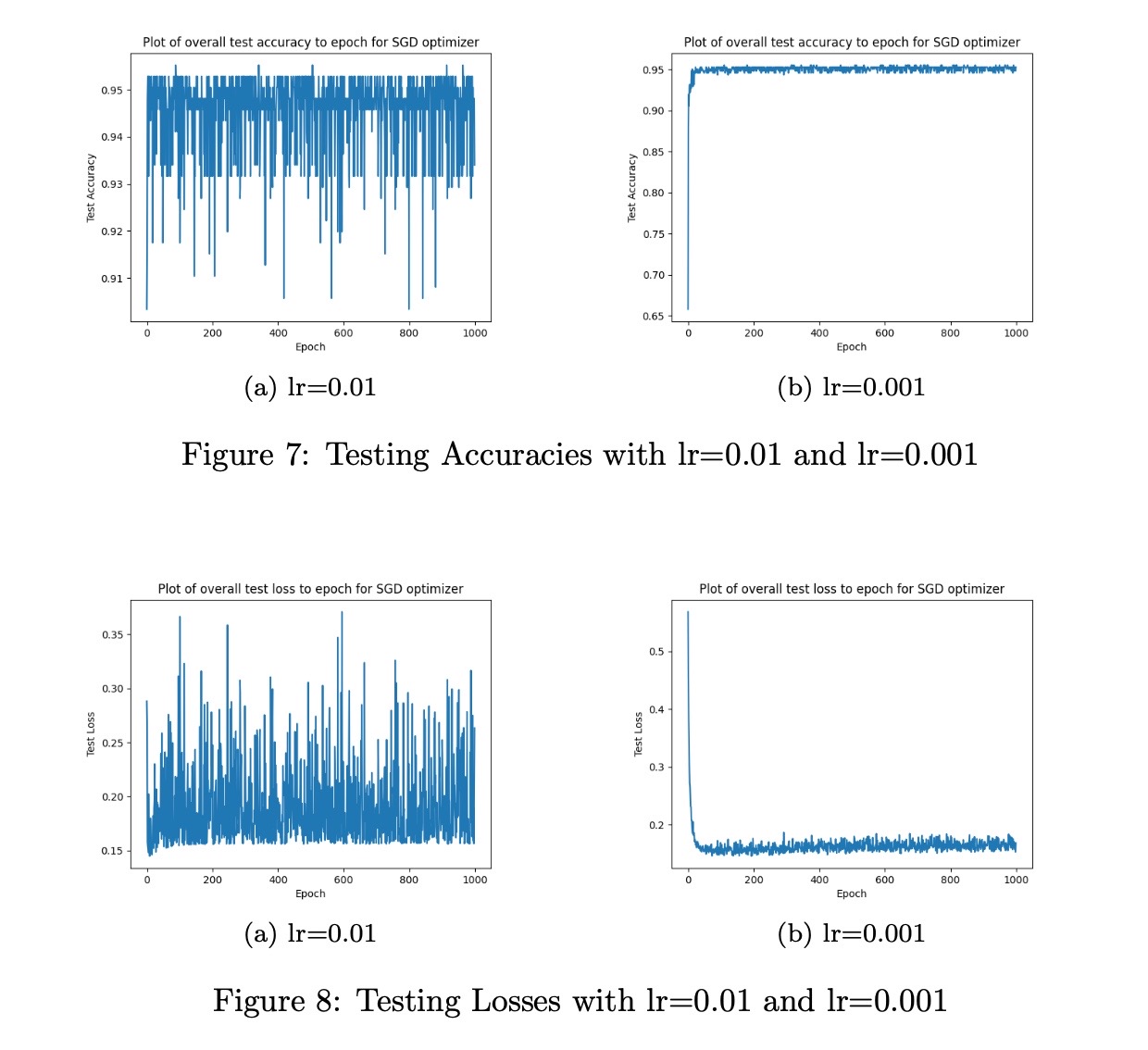
Here, α is the learning rate. I tried my model with different learning rates. I have observed that, when I select learning rate high, the steps get bigger and more rapid changes can be observed from the accuracy graphs.

Results

You can see the loss and accuracy plots of my model with epochs = [1000] and α=[0.01,0.001]